Physics 208 GH Midterm

Lecturer: Dr. Min Xu

Oct 30, 2002
LAST NAME: ___________________________________________________________________________________________________ FIRST NAME: __________________________________________________________________________________________________ SS# (last 4 digits): _____________________________________________________________________________________________

General Instruction

You have 2 hours to answer 5 questions on this exam. Work each problem only on the sheet provided for this problem, using the back if necessary. Please write the name and recitation section on each sheet at the top of the page.

You must indicate the reasoning and show all the steps.

If you are unable to obtain the answer to part of a problem and you need the answer to solve the subsequent parts, use an appropriate symbol for the answer to the previous part and solve in terms of that symbol.

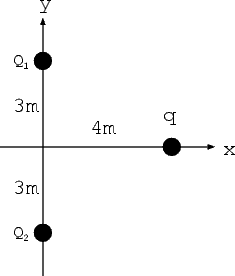
1. (20 points) Two point charges Q1 = Q2 = +25nC are located on (0, 3m) and (0,-3m) on the y-axis.


(a) (3 points) Find the electric field E(x) along the x-axis (magnitude and direction).
(b) (3 points) Find the electric potential V (x) along the x-axis.
(c) (3 points) Verify that E(x) = -dV- dx ^x.
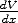
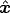(d) (3 points) Suppose a testing charge q = +1nC is put at position (4m, 0) on the x-axis. Find the electric potential energy of the above testing charge.
(e) (3 points) If the testing charge is released from rest at its initial position (4m, 0), it will escape. Why?
(f) (5 points) Find the escaping speed when this testing charge moves to infinity. Assume the mass of the testing charge is 10-10g.

PIC
Figure 1: Figure for question 1.

2. (20 points) A metal sphere with charge +q and radius ra is placed at the center of a metal spherical shell with net zero charge, inner radius rb and outer radius rc. Here ra < rb < rc.


(a) (10 points) Find the electric field E(r) for regions r < ra, ra < r < rb, rb < r < rc and r > rc.
(b) (5 points) Find the surface charge densities on the surfaces r = rb and r = rc.
(c) (5 points) Draw the electric field lines in all regions. Please note that the density of electric field lines represents the strength of the electric field.

3. (20 points) Following the previous problem. Now assume the spherical shell contains net charge -q. The sphere and the shell then form a capacitor.


(a) (5 points) Redraw the electric field lines in all regions.
(b) (5 points) Find the potential difference V ab between the sphere and the shell.
(c) (5 points) Find the capacitance C formed by the sphere and the shell.
(d) (5 points) What is the amount of electric potential energy stored in this capacitor.

4. (20 points) The battery for an IBM thinkpad maintains a voltage V = 16V with a current I = 4.5A in normal operations.


(a) (5 points) What is the effective resistance of this thinkpad?
(b) (5 points) Assume the wiring in this thinkpad can be approximated by an 18-gauge copper wire with a nominal diameter of 1.02mm (a wild simplification!), find the total length of the wire in this thinkpad. The resistivity of copper is 1.72�10-8_O_.m.
(c) (4 points) Find the current density.
(d) (6 points) Find the drifting speed of free electrons in the above wire. The density of free electrons in copper is 8.5 � 1028/m3. How long will a free electron take to travel the full loop?

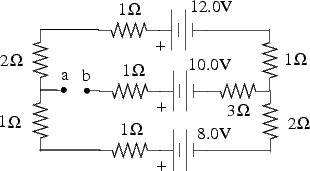
5. (20 points)


(a) (10 points) Find the potential of point a with respect to point b in the following figure. State which point has a higher potential.
(b) (10 points) If points a and b are connected by a wire with negligible resistance, find the current in the 12.0V battery.

PIC
Figure 2: Figure for question 5.